Table of Contents
Cobb-Douglas Production Function
The Cobb-Douglas Production Function is a particular form of the Production Function.
It takes the following form:
Q(L,K) = A Lβ Kα
- L:labor
- K:capital
- Q:output
- A>0
- 0<α<1
- 0<β<1
Properties of Cobb Douglas Production Function
- The marginal product is positive and decreasing.
- Output elasticity is constant, equal to α for L or β for K.
- Return to scale are α+β
Plot of a Cobb-Douglas production function:
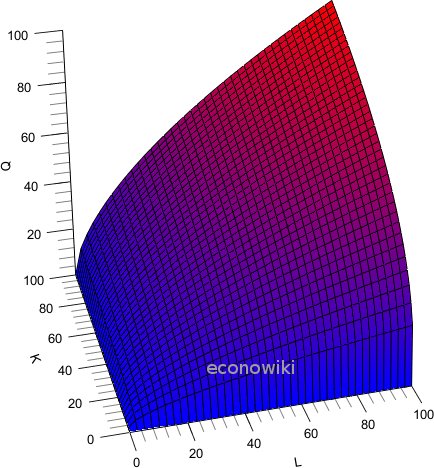
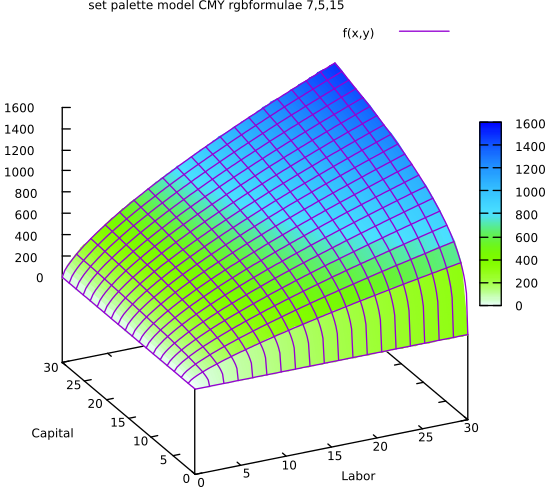
The marginal product is positive and decreasing
This behavior is usually seen in a lot of real world examples. To find the marginal product of a production factor, we derivate the total output with respect that factor. For example, to find the marginal product of capital:
∂Q / ∂K =
= α * (A Lβ ) K(α-1)
Given that α is positive and lower than 1, the marginal product is positive and decreasing.
Graphically:
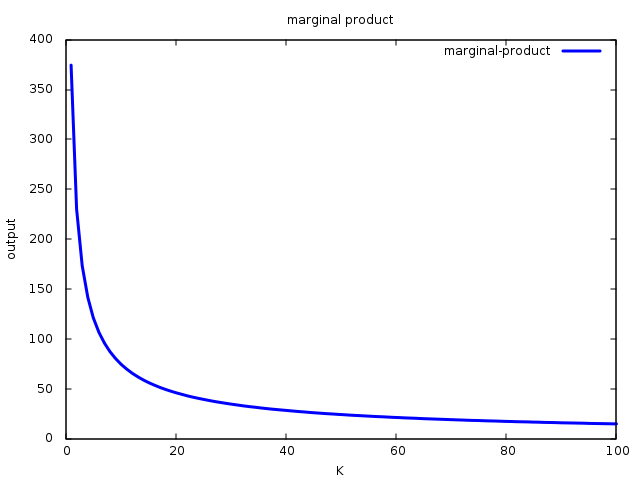
Output elasticity is constant
Output elasticity is defined as the percent change in output, when there is a percent change in one production factor.
In the case of the Cobb-Douglas production function, output elasticity is constant. Output elasticity of labor is β and output elasticity of capital is α.
Proof
By definition, output elasticity is:
(∂Q/Q) / (∂L/L) =
= (∂Q/∂L) / (Q/L) That is the marginal product of labor divided the medium product of labor.
= [ Aβ Lβ-1 ) Kα ] / [ A Lβ Kα / L ]
Given that 1/L is L-1 , ALβ Kα /L is ALβ-1 Kα . It follows that output elasticity is:
= AβLβ-1 Kα / ALβ-1 Kα
The only difference between the numerator and the denominator is β; then:
Output elasticity = AβLβ-1 Kα / ALβ-1 Kα = β
Return to scale are α+β
Returns to scale measure the proportional change in output, given a proportional change in the quantity of every factor of production.
Proof
If we increase every factor in a given constant c, the new output level will be:
Q' = A(cL)β (cK)α
= Acβ Lβ cα Kα
= cβ cα ALβ Kα
= cβ+α Q
This means that if we increase every production factor by c, the output level will increase in cβ+α .
If β+α = 1, the output will increase in c. In this case, the Cobb-Douglas production function has constant return to scale.
If β+α < 1, the proportional increase in output will be lower than the proportional increase in production factors. In this case, the Cobb-Douglas production function has decreasing returns to scale.
If β+α > 1, the proportional increase in output will be higher than the proportional increase in production factors. In this case, the production function has increasing returns to scale.
Discussion
If it is possible can someone post a real applicable example of how to calculate the elasticity of output with respect to labor and capital on Cobb Douglas function
Example function:
[1] Q=10 L^0.4 K^0.6Output elasticity (OE) with respect to K:
[2] (∂Q/∂K) / (Q/K)[3] (∂Q/∂K) = 10 L^0.4 0.6 K^-0.4[4] (Q/K) = 10 L^0.4 K^-0.4Then, the output elasticity is: [3]/[4] (notice that almost all components of [3] and [4] all the same, so they cancel each other.
[5] Output Elasticity = 0.6Complete case example should be better.