Table of Contents
Production Function Example
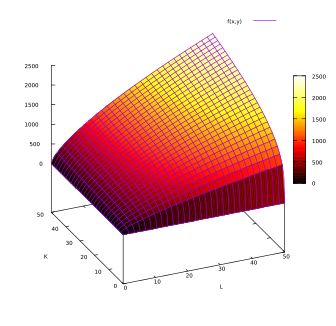
1- Example of a Cobb Douglas Production Function
The Cobb Douglas Production Function is widely used in economic models. It takes the following form:
Q(L,K) = A Lβ Kα
L:labor
K:capital
Q:output
A>0
0<α<1
0<β<1
The main characteristics of the Cobb-Douglas production function are:
- The marginal product is positive and decreasing.
- Output elasticity is constant, equal to α for L or β for K.
- Return to scale are α+β
This example is as follows:
A = 50
α = 0.7
β = 0.3
The plot of this example is:
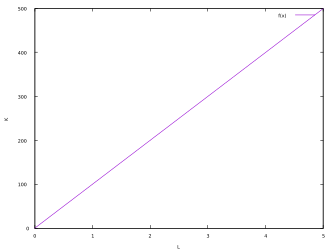
2- Example of a Linear Production Function
This is the simplest example. In this example, the output is in a direct linear relationship with the quantity of a single input. For example, if each robot can produce 100 T-Shirts per hour, and there are no other inputs, the production function will be:
Q = 100 K
Where:
- Q = Quantity of T-Shirts per Hour
- K = Number of Robots
The plot of this example is:
Example 3: One Input Production Function with Diminishing Returns
In this example we will see the case of a production function that has only one factor of production: robots: But if we keep adding robots, the output of each robot will decrease. Maybe because the robots start to chat with each other and it's productivity decreases ![]()
In this example, the production function is:
Q = 100 * K 0.9
If there is only one robot, the output will be the same as in the linear example: 100. But if we add a second robot, the output will be lower:
100*20.9= 186
Where in the linear example, two robots would have produced 200 T-Shirts
The charts of both examples is:
We can see that as we keep adding robots, the difference in the quantity produced between the diminishing returns example and the linear example keeps growing.
Example 4: CES Production Function
This production function has, as the name says, a constant elasticity of subsitution. An example of this production function, using two inputs is:
Q = F (a * Kα + (1 - a) L α)1/a
Example 5: Fixed Proportions Production Function
In a fixed proportions production process, the inputs are needed in a fixed relationship. For example, if we need one person per computer. If we add an additional person, and we do not add an additional computer, output will not increase. The same will happen if we add an additional computer, but we do not add an additional person. In this example, the proportions are 1:1, but there can be other proportions that will also match the fixed proportions production function, for example, if we need 1 person to control 10 robots.
Example of a fixed proportions production function:
Q = min {L,K}
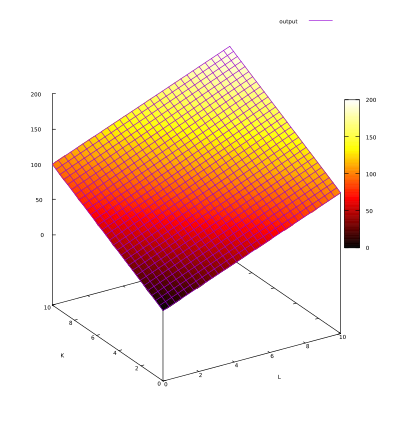
Example 6: Perfect Substitutes Production Function
In the Perfect Substitutes Production Function, one input can be substituted for another without any effect in the quantity produced.
Example:
Q = aL + aK
If we increase L by 10 and at the same time, we decrease K by 10, the output will be the same.
Discussion