en:proof-of-the-law-of-cosines
Proof of The Law of Cosines
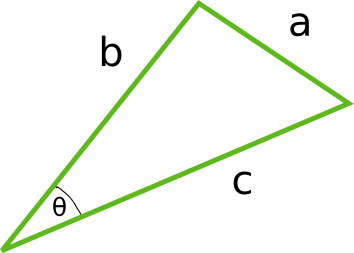
Law of Cosines: a2 = b2 + c2 - 2bccos(θ)
Proof
Divide the triangle into 2 right angle triangles:
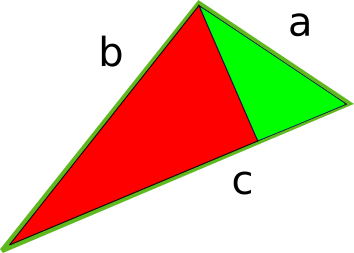
Using trigonometry, the sides of the green triangle are
- Longest side: a
- Side on the left: b . sin θ ; because the sine of θ is opposite divided the hypotenuse, and the opposite is the length of this side. Then, the length of this side is the hypotenuse multiplied by the sine of θ
- Side on the right: *c - b cos(θ) ; we must subtract from the length “c”, the part of c that is occupied by the red triangle. We know that, in the red triangle, cos θ is the adjacent side divided the hypotenuse. The adjacent is the “base” of the red triangle, and it is cos θ multiplied by the hypotenuse. The hypotenuse is b. Then, the base of the red triangle is (cos θ)b. So, the length of the “base” of the green triangle is c - b.cos θ
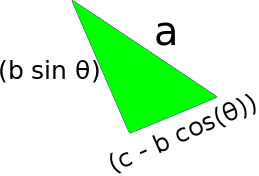
Using the Pythagorean Theorem:
a2 = (b sin θ)2 + (c - b cos(θ))2
= b2 sin 2 θ + c2 - 2cbcos(θ) + b 2 cos 2 θ
= b2 (sin 2 θ + cos 2 θ) + c2 - 2cbcos(θ)
Knowing that (sin 2 θ + cos 2 θ = 1) 1)
= b2 * 1 + c2 - 2cbcos(θ)
a2 = b2 + c2 - 2cbcos(θ)
en/proof-of-the-law-of-cosines.txt · Last modified: 2017/07/14 10:47 by federico
Discussion